Tutorial 4

Tutorial Summary

Core topics:

Improving visualisation
Measures of variation

Advanced topics:

More about loops

In this tutorial we will cover descriptive statistics that we can use to measure variation in our data and look at how to improve your visualisations.

Improving visualisations

Back in Tutorial 4 you created some visualisations (pie chart, bar chart and histograms) using the plot() function of a Pandas DataFrame. This function actually uses Matplotlib to all the plotting. For instance, we can plot a histogram of Global Studies student heights:

# Create a histogram
gs_intro_survey['Height'].plot(kind='hist', bins=20, color='skyblue', edgecolor='black')

# Adding labels and title
plt.xlabel('Height')
plt.ylabel('Frequency')
plt.title('Height Distribution Histogram')

We can equivalently create the same plot using Matplotlib directly:

# Create subplots
fig, ax = plt.subplots()

# Create a histogram
ax.hist(gs_intro_survey["Height"], bins=20, color='skyblue', edgecolor='black')

# Adding labels and title
ax.set_title('Heights')
ax.set_xlabel('Height')
ax.set_ylabel('Frequency')

Why would we want to use Matplotlib directly? By using Matplotlib directly we can create more elaborate visualisations, but requires more coding!

For example we can make a figure with 3 subplots that displays the same data in 3 different ways:

# Select the heights from the dataframe
heights = gs_intro_survey["Height"]

# Create subplots
fig, axes = plt.subplots(nrows=3, ncols=1, figsize=(8, 10))

# Plot histogram
axes[0].hist(heights, bins=20, color='skyblue', edgecolor='black')
axes[0].set_title('Histogram')

# Plot rug plot
axes[1].plot(heights, np.zeros_like(heights), '|', color='green', markersize=10)
axes[1].set_yticks([])  # Hide y-axis markers and numbers
axes[1].set_title('Rug Plot')

# Plot box plot
axes[2].boxplot(heights, vert=False)
axes[2].set_yticks([])  # Hide y-axis markers and numbers
axes[2].set_title('Box Plot')

# Adjust layout for better spacing
plt.tight_layout()

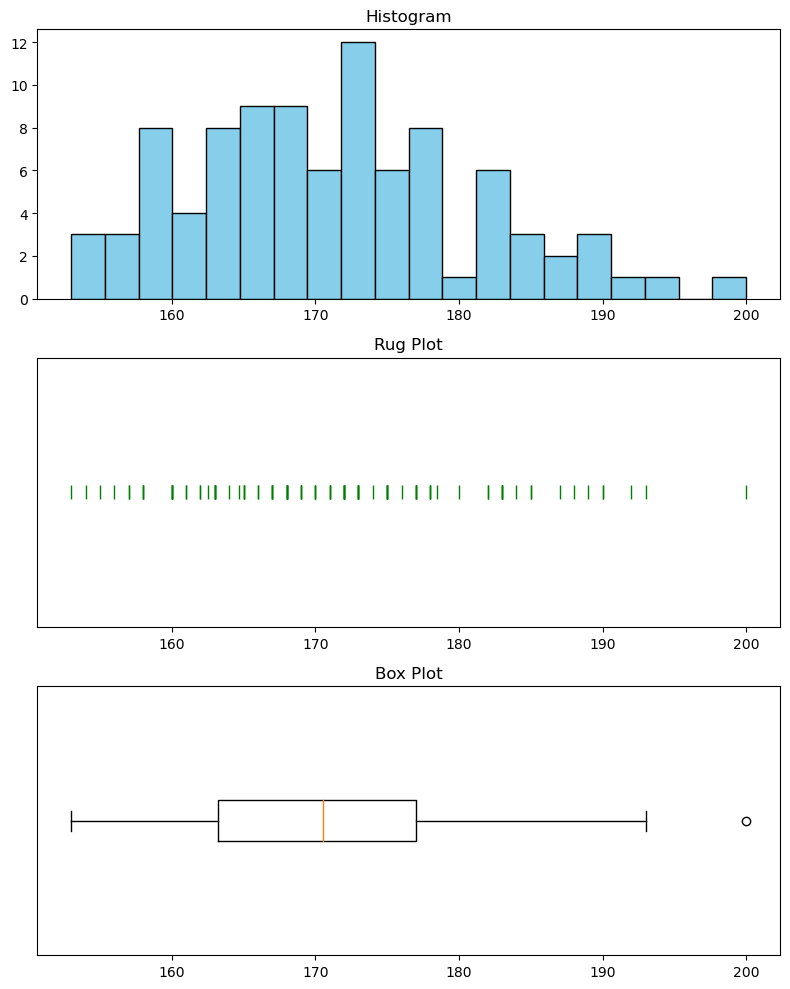
three plots

Exercise 1: Try the above code for yourself. Remember to import the necessary libraries and load the gs_intro_survey data.

Exercise 2: Look at each plot. What information do you think each plot shows?

Exercise 3: Experiment with the code and check the documentation to see how much of the code you can understand. Some tips and ideas to try:

The subplots() function returns two things:
1. a figure that contains the whole visualisation, which we store in the fig variable, and
2. an array of axes that contains each individual plot, which we store in the axes variable
Try commenting out a line using # at the beginning so that python ignores the code on that line
Try adjusting the figure size and arranging the plots in three columns instead of three rows.
Add labels to the (horizontal) x-axis and (vertical) y-axis.
Experiment with different colours

You can annotate your visualisations to indicate certain values using axvline() and text(). For instance, you can use the following code in the previous example:

axes[0].axvline(184, color='black')
axes[0].text(184, 8,"Leto's height",rotation=90, 
             backgroundcolor='white', horizontalalignment='center')

Code for a single figure must all be contained within the same cell code in your notebook. It won’t work across different cells

Exercise 4: Use axvline() and text() to annotate the figure with the averages that we covered last week.


Good visualisations help convey your messages.¹

Measures of variation

Measures of variation are statistical indicators that describe the spread or dispersion of a set of data points. They help us understand how much individual data points deviate from averages, such as the mean or median. Here’s an overview of some common measures of variation:

Range: The range is the simplest measure of variation and is calculated as the difference between the maximum and minimum values in a dataset. It is sensitive to outliers and may not accurately represent the overall variability if extreme values are present.

\[\rm Range = Maximum Value - Minimum Value.\]

Variance: The variance measures the mean squared distance of each data point from the mean. A higher variance indicates greater variability, and a lower variance suggests that the data points are closer to the mean.

\[\textrm{Variance}(\sigma^2)= \frac{\sum_{i=1}^n (x_i−m)^2}{n},\]

where $n$ is the number of data points, $x_i$ represents each data point, and $m$ is the mean.

Standard Deviation: The standard deviation is the square root of the variance. It is a more interpretable measure of spread, as it is in the same units as the original data. Like variance, standard deviation is sensitive to outliers, but it is widely used due to its ease of interpretation.

\[\textrm{Standard Deviation}(\sigma) = \sqrt{\frac{\sum_{i=1}^{n} (x_i - m)^2}{n}}\]

where $x_i$ represents each individual data point, $m$ is the mean and $n$ is the number of data points.

Quartiles: are values that divide a dataset into four equal parts. They help us understand the distribution of the data and identify key points. There are three quartiles in a dataset:

First Quartile (Q1): This is the value below which 25% of the data falls. In other words, if you order your data from smallest to largest, Q1 is the value at the 25% mark. Also known as the 25th percentile.
Second Quartile (Q2): This is the median of the dataset. It’s the middle value when the data is sorted. Fifty percent of the data points are below Q2, and fifty percent are above it. Also known as the 50th percentile.
Third Quartile (Q3): This is the value below which 75% of the data falls. Like Q1, if you order your data, Q3 is the value at the 75% mark. Also known as the 75th percentile.

Interquartile Range (IQR): The interquartile range is a measure of statistical dispersion, or, in simple terms, the range of the middle 50% of the data. It is less sensitive to extreme values than the range, variance, or standard deviation. The IQR is the difference between the third quartile (Q3) and the first quartile (Q1). It represents the spread of the central portion of the data.

\[\rm IQR=Q3−Q1 .\]

These measures of variation provide different perspectives on the distribution of data. Researchers and statisticians choose the most appropriate measure based on the characteristics of the dataset and the goals of their analysis.

Exercise 5: Write some code using variables x and m that subtracts a value x from m and returns the answer.

Exercise 6: Write some code using variables s and n that divides a number s by another number n and returns the answer.

Exercise 7: Write some code that calculates the mean of a list of numbers without importing any modules. Which module could you import to test that your code works correctly? Test that your code works correctly.

Exercise 8: Using code you have written, can you write some code that calculates the variance?

Exercise 9: Think about the definition of variance. The variance aims to capture information about how much we expect values to be different from the mean. Think about the code and/or the formula for variance above. Notice that we compare each data point to the mean. Why is it necessary to square the difference between each data point and the mean? Experiment with the function you wrote to see what happens if you do not square it.

Exercise 10: The standard deviation is considered more easy to interpret because it is in the same units as the data. Use the code below to generate some data and investigate the standard deviation:

r = 1 
x = np.zeros(10)   # create a dataset of 10 values
x[:5] = m - r
x[5:] = m + r

Look at the values of x of the function as you change the value of r. How does the mean and standard deviation change as you vary the value of r?

Hint: you can use numpy.mean(x) and numpy.std(x) to calculate the mean and standard deviation

Exercise 11: Annotate the distribution of heights from earlier to indicate these measures of variation. The statistics functions in numpy will be useful.

Exercise 12: Using everything you’ve learned this week, can you now determine what information the boxplot shows you?


And this is why the box plot was invented.²

More about loops (ADVANCED)

A for loop tells Python to execute some statements once for each value in a list, a character string, or some other iterable. Back in Tutorial 2 we introduced for loops with a simple example of greeting a list of people by name:

names = ["Alice", "Bob", "Charlie", "Deborah"]  # define a list of names

for name in names:    # you can read this as "for each name in the list names"
    print(f"Hello {name}") # python runs this code (the same line as before)

The essential ingredients of a for loop are a List, a loop variable, and a body:

The list¹ is the sequence of items we want to loop over and repeat an action (or set of actions).
The loop variable is set to the current element in the list and changes at each iteration of the loop.
The body specifies what action to take for each element in the list. The body performs the action (or set of actions) on the current value of the loop variable.

ages = [7, 43, 18, 25]  # The List: the items we loop over

for age in ages:    # The Loop Variable: `age` is the loop variable
    # The body: is in the next two lines of code and applies actions to 
    # the loop variable that is assigned to a value from the list.
    age_in_five_years = age + 5
    print(f'Someone who is {age} will be {age_in_five_years} in five years')

It is important to remember that the first line of the for loop must end with a colon :, and the body must be indented.

The colon at the end of the first line signals the start of a body of actions is about to start.
Indentation indicates which lines are are part of the body. Lines with the same amount of indentation form part of the same body (the same as if and else conditional statements). Any consistent indentation will work, such as a Tab or a set of Space characters. A common practice is to use four spaces per indentation.

You can repeat something a number of times using a list of numbers, e.g.,

for number in [0, 1, 2, 3, 4]: # for each number in this list
    print(f"Hello {number}")   # print hello
print(f"Goodbye {number}")

Instead of writing out a list of numbers you can use the Python function range()

Exercise 13: Try the example above, but replace the list [0, 1, 2, 3, 4] with:

range(5)
range(10)
range(2,14)
range(2,14,2)

What is happening in each case? What does the range() function do?

Exercise 14: Try these two versions of code:

for number in [0, 1, 2, 3, 4]: # for each number in this list
    print(f"Hello {number}")   # print hello
print(f"Goodbye {number}")

for number in [0, 1, 2, 3, 4]: # for each number in this list
    print(f"Hello {number}")   # print hello
    print(f"Goodbye {number}")

How is the output different? Can you see why?

Exercise 3: Use the range() function to create a for loop that outputs the name and age of each person using two lists:

names = ["Alice", "Bob", "Charlie", "Deborah"]
ages = [7, 43, 18, 25]

For example, the output in each iteration of the loop should be something like Alice is 7 years old .

Remember that you can index lists using square brackets [], e.g., names[0] returns the first name in the names list.

Rock paper scissors (part 4)

Now we will use a for loop to improve our game of Rock, Paper, Scissors that we started in Tutorial 3. Often when we play Rock, Paper, Scissors we play a series of rounds, e.g., best of 3 or best of 5.

Exercise 15: Use a variable n_rounds to set a number of rounds to play and a for loop to play Rock, Paper, Scissors n_rounds times. Keep score and output the number of wins that the computer and the user have at the end of the game. Use an appropriate visualisation to summarise the number of wins by the computer and user.

While loop

Using a for loop we can repeat a set of actions either a predetermined number of times (i.e., using range()) or once per element in a list. However sometimes we would like to repeat a set of actions until a specific condition is satisfied.

In this case we can use a while loop. The while loop repeats until a condition is no longer satisfied. We can specify a condition in a similar way to if statements. For example, we can create a while to count until it reaches 5.

count = 1
while count <= 5:
    print(count)
    count = count + 1

Just like a for loop, a while loop has a loop variable and a body, but instead of a list it has a conditional statement. A while loop will continue to repeat while the conditional statement is True and terminates when the conditional statement is False.

Here is some code that asks a user to solve a simple maths problem that has two solutions.

answer = 0
attempts = 0

while answer not in [2, 4]:
    answer = int(input('Enter an even number between 1 and 5'))
    attempts = attempts + 1

print(f'Well Done! Correct after {attempts} attempts')

Exercise 16: Try the example above in your notebook and try to work out what each line of code does. Include your explanation in your notebook.

Rock paper scissors (part 5)

At the moment your game of Rock, Paper, Scissors will accept invalid or misspelled inputs from the user. We can use a while loop to ask the user to input something until a valid input is given.

Exercise 17: Use a while loop to check that a user correctly inputs either Rock, Paper or Scissors and ask for another input in the case they do not enter a valid input.

Compound interest

Exercise 18: Calculate the interest on a loan. Let’s say you want to borrow 100 Euros from a friend. Your friend agrees, but says they will charge you 1% interest per day until you pay them back.

First let’s calculate the amount you owe them after one day:

percentage_per_day = 1.0 
loan = 100 # the amount you owe
interest = loan * percentage_per_day / 100 # this calculate the amount of interest after one day
loan = loan + interest # this is the new amount that you owe your friend after one day
print(f"You owe {loan} Euros")

Use a For loop to work out how much would you owe your friend if you waited one year to pay them back?

Exercise 19: Use a while loop to determine how long it takes to repay the loan?


	Compound interest isn’t magic¹

Investing by xkcd licensed under CC BY-NC 2.5 ↩ ↩² ↩³
Geothmetic Meandian by xkcd licensed under CC BY-NC 2.5 ↩